データベースのための基礎理論
- 集合(set): 「もの」の集まり. 数, 文字, 記号など
- 要素(element): 集合に属する「もの」のこと. 元とも呼ぶ a∈A
- 空集合(empty set): 何も要素を含まない集合 A=ϕ
- 例)
A=−6,−5,−4,1,2,6A=a,aba,ababa,abababa,…A=情報工学科,機械工学科,電気工学科,工業化学科,建築学科A=0,1,1×集合ではない
全く同じ要素が2つ以上含まれている場合、それは集合ではない.
集合演算
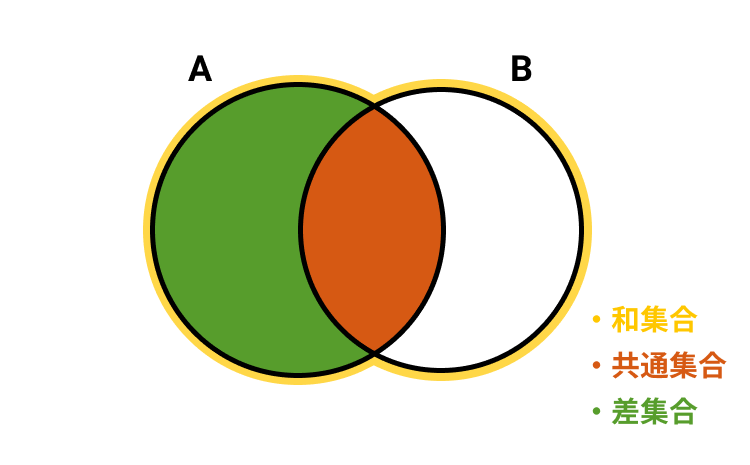
- 和集合 A∪B=x|x∈A∨x∈B
- 共通集合(積集合) A∩B=x|x∈A∧x∈B
- 差集合 A−B=x|x∈A∧x∉B
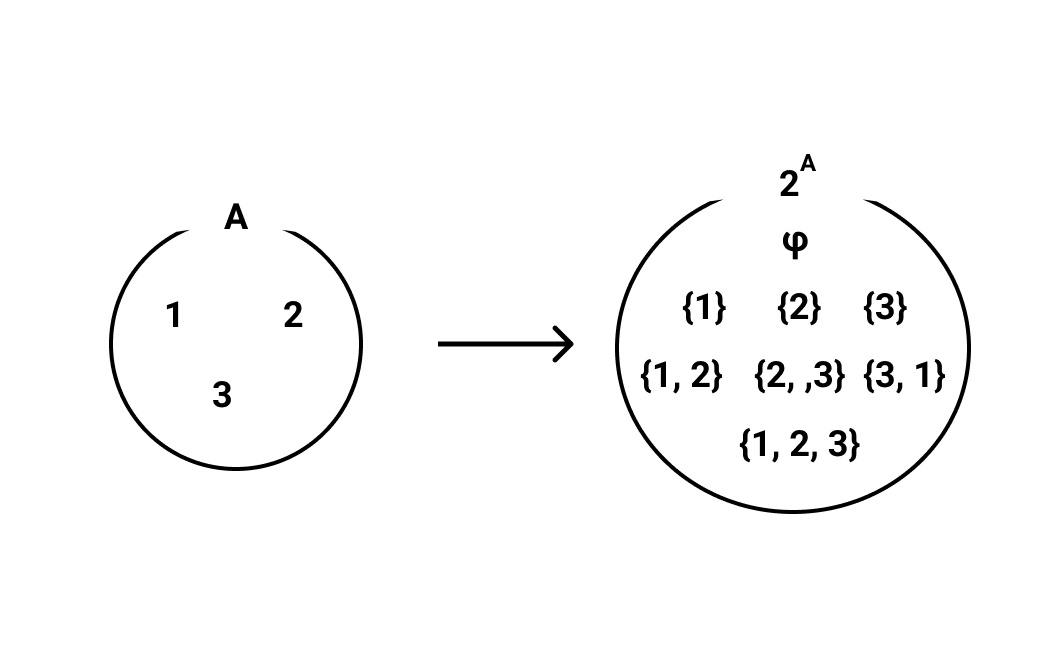
- べき集合 2A=X|X⊂A
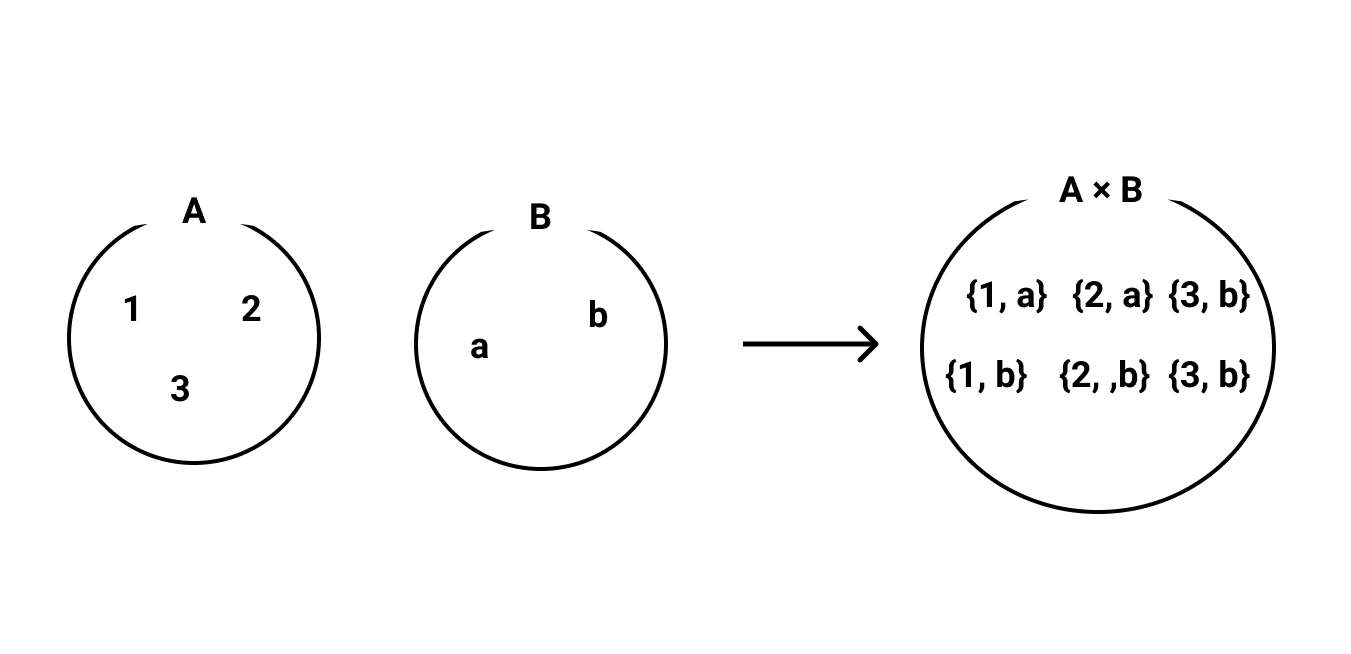
- 直積集合 A×B=(a,b)|a∈A∧b∈B
リレーショナルデータモデル
実世界のモノ・概念を表(=リレーション)として表現
- 属性(attribute): データの種類(表でいうところの列)
- タプル(tuple): データの組(表でいうところの行)
- リレーション(relation): タプルの集合, インスタンス
注意点
- 同じタプル(行)が重複して、リレーション(表)の中に現れることはない(リレーションはタプルの「集合」だから)
- タプル(行)の順序に意味がない
- 属性(列)の順序には意味がない
第1正規形リレーション
単純な値でできている表
- 表の中に表やリストがない(入れ子型リレーションではない)
- 各行の構造が共通している
リレーショナルデータモデルで扱うリレーション
例)
| 年 | 国税収入総額 | 国税収入増減比 | 酒税収入総額 | 酒税収入増減比 |
|---|---|---|---|---|
| 1980 | 284 | - | 14.2 | - |
| 1990 | 628 | 221 | 19.4 | 137 |
| 2000 | 527 | 84 | 18.2 | 94 |
| 2010 | 437 | 83 | 13.9 | 76 |
非正規形リレーション
- タプルの構造が行ごとに異なる
- 表の項目が表やリストになっている
数学的な定義
リレーション名: ( R )
属性名: (A_1, A_2, …, A_n)
nは次数(degree)
リレーションスキーマ: (R(A_1, A_2, …, A_n))
ドメイン(定義域): ( D_1, D_2, …, D_n)
属性値の定義域(どういう型の値か, どのような制約があるかを指定)
直積集合: (D_1 \times D_2 \times \cdots \times D_n )
タプル: (t \in D_1 \times D_2 \times \cdots \times D_n )
直積集合の要素
リレーション(インスタンス): (R \subset D_1 \times D_2 \times \cdots \times D_n)
直積集合の有限部分集合, リレーションの行の数のことを濃度(cardinality)と呼ぶ.
リレーションと整合性制約
データベースとして矛盾なく健全である状態を保つための条件や制約
ドメイン制約(domain constraint)
属性値が, その属性のドメインに含まれる(データ型が一致)
- 年: 正の整数, 月: 1 ~ 12, 日: 1 ~ 31
- 氏名: 文字列
例) 学生テーブル
キー制約または一意性制約(unique constraint)
- 属性または属性の集合において、同じ属性値がリレーションの中で重複して現れることがない
| 学籍番号 | 所属学部 | 氏名 | 電話番号 | 住所 |
|---|---|---|---|---|
| 4619001 | 46 | 理大 太郎 | 03-1234-0000 | 東京都新宿区神楽坂… |
| 4619005 | 46 | 鈴木 一郎 | 03-5678-0000 | 東京都葛飾区新宿… |
| 4619002 | 44 | 理大 花子 | 090-123-0000 | 東京都新宿区神楽坂… |
| 4619001 | 46 | 田中 一郎 | 070-123-0000 | 千葉県松戸市… |
学籍番号がUNIQUEのとき、このリレーションは制約違反
キー(key)
- スーパーキー(super key): タプルを一意的に特定できる属性や属性の集合
- 候補キー(candidate key): 他のスーパーキーを含まない極小の属性集合
- 主キー(primary key): 候補キーから任意に選択した一つ(NULLを含まない)
- 複合主キー: 主キーを構成する属性集合(主キーが2個以上の属性から構成される場合)
| 学籍番号 | 所属学部 | 氏名 | 電話番号 | 住所 |
|---|---|---|---|---|
| 4619001 | 46 | 理大 太郎 | 03-1234-0000 | 東京都新宿区神楽坂… |
| 4619005 | 46 | 鈴木 一郎 | 03-5678-0000 | 東京都葛飾区新宿… |
| 4619002 | 44 | 理大 花子 | 090-123-0000 | 東京都新宿区神楽坂… |
| 4619008 | 46 | 田中 一郎 | 070-123-0000 | 千葉県松戸市… |
ここで、
{学籍番号, 氏名}: スーパーキーであるが候補キーではない
{学籍番号}: 候補キー
実体整合性制約(entity integrity constraint)
属性(または属性の集合)がNULL(空値)を取らない
- 主キーはNULLを取らない、候補キーはNULLをとっても良い
| 学籍番号 | 所属学部 | 氏名 | 電話番号 | 住所 |
|---|---|---|---|---|
| 4619001 | 46 | 理大 太郎 | 03-1234-0000 | 東京都新宿区神楽坂… |
| 4619005 | 46 | 鈴木 一郎 | 03-5678-0000 | 東京都葛飾区新宿… |
| 4619002 | 44 | 理大 花子 | 090-123-0000 | 東京都新宿区神楽坂… |
| NULL | 46 | 田中 一郎 | 070-123-0000 | 千葉県松戸市… |
これは学籍番号がNOT NULLであるため実体整合性制約に違反
参照整合性制約(reference integrity constraint)
- 外部キー(foreign key): NULLを除いて他リレーションの主キーにある属性値を取る属性